2.1 半导体致冷器原理型的数学模型:

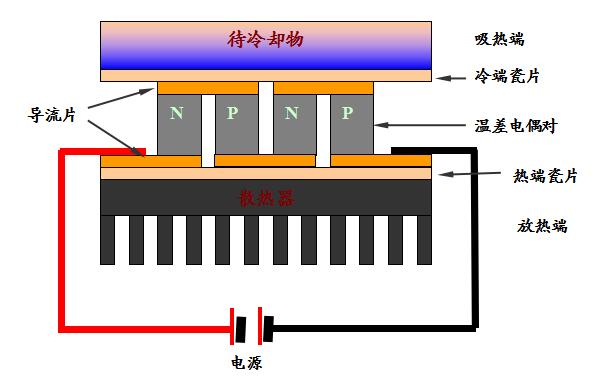
如图所示的是一个最简单、最基本的温差电器件,由N、P两种类型的半导体温差电材料经电导率较高的导流片串联构成。当电流流过回路时,将在接头A处发生吸热,而在接头B处放热,使得T2>T1,因而在A、B两端建立温差ΔT=T2-T1,其作用就是一个制冷器。
根据帕尔贴效应建立在冷端A处的热平衡方程,可获得该接头处单位时间从外界进入的热量(制冷量)Qc为:
Qc=αNP T1I – 0.5I2R – k(T2 – T1
其中R为N、P电偶臂的电阻,
αNP 为N、P电偶臂的温差电动势总和,与制冷器的电偶臂对数有关
I为通过回路的电流,
k为电偶臂的热阻总和。
2.2 温差电优值Z
为了评价温差电材料和器件的各种性能,可以引入一个与温差电材料有关的概念:温差电优值Z。
对于温差电材料而言,Z=α2.σ/λ
其中α为材料的赛贝克系数,也就是温差电动势,
σ为材料的电导率,λ为材料的热导率。
对于温差电器件而言,Z =αNP2/ R.k
2.3 最大温差电流和最大温差
温差电制冷器的一个重要性能参数是器件两端所能建立的温差ΔT=T2-T1。显然,这个温差与制冷器的制冷能力和外加热负荷有关。
利用器件的冷端热平衡方程,可以求得
ΔT=(αNP T1 I – 0.5I2R – Qc )/ k
对于制冷器无外加热负载的情况即Qc=0,令d(ΔT)/dI=0,可以求得相应于ΔT取极值时的最佳电流IT为
IT=αNP T1/R
当制冷器工作在这个最佳电流时,具有的最大温差ΔTmax为
ΔTmax=0.5 ZT 12
以上是从制冷器冷端热平衡方程中推导出的最大温差电流和电偶对两端的最大温差的计算方法。在厂商样本中和实际应用时,往往将其换算成以热端温度T2为参照值的数据,也就是定义:
最大温差电流Imax:在热端温度恒定为Th(通常定义为27℃)、负载Qc为0的情况下可以获得最大温差ΔTmax即最低冷端温度Tc max时应输入的电流值。
最大温差ΔTmax:在热端温度恒定为Th(通常定义为27℃)、负载Qc为0、通以最大温差电流的情况下,制冷器可以获得的温差值。
如果要实际测量这两个参数,需要在真空条件下测量。我公司样本中提供的数据指的就是在真空条件下测的数据。
2.4 最大产冷量Qcmax:
制冷器工作时单位时间内从外界吸入的热量成为产冷量,单位是W。当材料的特性αNP、R、k一定时,器件的产冷量与通过器件的电流和两端的温差有关;对于不同的外加电流和温差条件,其产冷量是不同的。
在制冷器冷端热平衡方程中,令dQc/dI=0,可以获得相对于Qc取极值时的最佳电流值Iq为
Iq= IT=αNP T1/R
相对于的产冷量Qc为
Qc=0.5αNP 2T12/R – k(T2 – T1)
进一步,若定义制冷器工作在最佳电流Iq工况下,且器件两端的温差为0时制冷量为器件的最大产冷量为Qcmax,则
Qcmax=0.5αNP 2T12/R
从上式中可以看出,最大产冷量也是温差的函数,我公司所给出的样本中的最大产冷量是指热面温度Th=27℃时标定的最大产冷量。
2.5 制冷效率COP
制冷器的制冷效率COP定义为:COP=Qc/P
Qc为冷端吸热量;P为制冷器输入功率.
制冷器两端的外加电压V应等于电偶臂上的电压降VR=IR,加上抵抗温差电压所需的电压降Vs=αNP(T2-T1),即
V=VR + Vs = IR + αNP(T2-T1)
由此可得制冷器的输入功率为:
P = VI = I2R + αNP(T2-T1)I
进而可获得制冷器的制冷效率COP
COP=[αNP T1 I – 0.5I2R – k(T2 – T1)]/[ I2R + αNP(T2-T1)I]
从式中可以看出,制冷效率COP不仅与器件的特定参数(αNP 、R 、k)有关以外,还与其具体工作状态(T1、T2-T1、I)有关。


 日期:2020-12-14
日期:2020-12-14